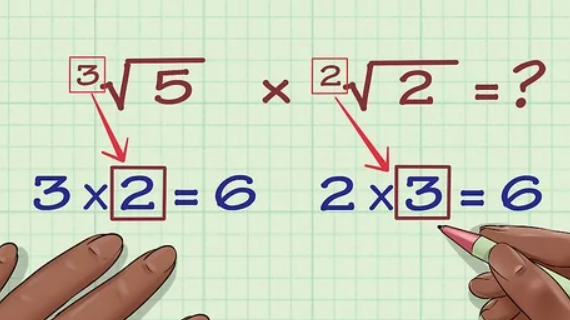In this article, we are discussing Multiplying radicals and complete lesson. The world of radicals might seem like a tangled forest of roots and symbols, but wait! Multiplying these enigmatic creatures holds hidden beauty and surprising simplicity. Forget about clunky calculators and embrace the elegance of manipulating square roots, cube roots, and beyond. In this exploration, we’ll weave our fingers through the roots, peeling back the layers of notation to reveal the fundamental rules that govern their playful dance of multiplication. Join me as we unlock the secrets of radical multiplication, transforming seemingly cryptic expressions into harmonious symphonies of numbers!
Parts of a Radical and Square Roots:
Here’s a breakdown of the parts of a radical and square roots, accompanied by equations:
Anatomy of a Radical:
- Radical symbol: The symbol √, resembling a checkmark, indicates a root.
- Radicand: The number or expression inside the radical symbol.
- Index (optional): A small number written above the radical symbol, denoting the type of root. If absent, it’s assumed to be 2 (square root).
Square Roots:
- Square roots, indicated by √ or √2, represent the number that, when multiplied by itself, produces the radicand.
- Example: √9 = 3, because 3 x 3 = 9
Equations with Square Roots:
- Solving for x: √x = 6
- Square both sides to eliminate the radical: (√x)² = 6²
- Simplify: x = 36
- Combining like terms: 3√5 + 4√5 = 7√5
- Multiplying radicals: √2 x √5 = √(2 x 5) = √10
Key Points:
- Only positive numbers have real square roots.
- Negative numbers have imaginary square roots, involving the number “i”.
- Simplifying radicals involves finding perfect square factors within the radicand.
- Multiplying square roots involves multiplying the radicands and keeping the same index.
Additional Information:
- Other common roots include cube roots (√3), fourth roots (√4), and so on.
- Radicals can also involve variables and expressions.
- Simplifying radicals often involves factoring and using rules of exponents.
Multiplying Radicals: A Symphony of Roots:
The realm of radicals, with their enigmatic symbols and hidden depths, can seem daunting at first glance. But fear not, for within lies a secret language, a melody of equations waiting to be unraveled. In this journey, we’ll learn the art of multiplying radicals, transforming seemingly cryptic expressions into harmonious symphonies of numbers.
The Essential Steps:
- Isolate the Radicands: Begin by separating the radicals from any surrounding coefficients. For example, if you have 3√2 and 5√7, your starting point becomes √2 and √7.
- Multiply the Radicands: Treat the radicands like any other numbers and simply multiply them together. In our example, √2 x √7 = √(2 x 7).
- Simplify the Radicand (Optional): Look for perfect squares within the resulting radicand. If you find any, factor them out and move them outside the radical symbol. Remember, a number’s square root multiplied by itself equals the original number. In our case, (2 x 7) has a perfect square factor of 2, so you can rewrite the expression as √(2 x 7) = √(2²) * √7 = 2√7.
- Combine Like Terms (Optional): If your expression involves multiple radicals with the same index, you can simply combine them by adding or subtracting their radicands. For instance, 2√5 + 3√5 = (2 + 3)√5 = 5√5.
Remember:
- You can only multiply radicals with the same index (e.g., √2 and √2, not √2 and √3).
- When simplifying, watch out for non-perfect square factors within the radicand. They need to stay inside the radical symbol.
- These basic principles can be applied to multiply radicals with more complex radicands and multiple levels of nesting.
Beyond the Basics:
Multiplying radicals unlocks a deeper understanding of their properties and behavior. It opens doors to solving equations involving radicals, simplifying expressions, and exploring advanced mathematical concepts. So, embrace the challenge, unravel the melody of multiplication, and let the music of the radicals guide you through this beautiful and fascinating realm.
Using Radical Notation:
Radical notation is a mathematical shorthand that allows us to express roots of numbers concisely and powerfully. It’s like a secret code that unlocks a world of numerical relationships and intricate calculations! Let’s dive into its key elements and how to use it effectively:
The Building Blocks:
- Radical symbol: √, resembling a checkmark, indicates a root.
- Radicand: The number or expression inside the radical symbol, representing what we’re taking the root of.
- Index (optional): A small number written above the radical symbol, specifying the type of root. If absent, it’s assumed to be 2 (square root).
Common Examples:
- √25 = 5 (square root of 25, which is 5)
- ³√8 = 2 (cube root of 8, which is 2)
- √(x + 5) (square root of the expression x + 5)
Using Radical Notation in Action:
- Representing roots concisely: √5 is much neater than “the square root of 5.”
- Writing equations: ³√x – 4 = 2 (cube root of x minus 4 equals 2)
- Expressing complex roots: √-1 = i (square root of -1, represented by the imaginary unit i)
- Simplifying expressions: √18 = √(9 x 2) = 3√2 (simplifying square root of 18)
- Solving equations: √x = 7, square both sides to get x = 49
Beyond the Basics:
Radical notation extends beyond square and cube roots, allowing us to represent any root! It also combines with other mathematical operations like addition, subtraction, multiplication, and division, enabling us to create and manipulate complex expressions.
Remember:
- Radicals are a gateway to exploring irrational numbers, roots of polynomials, and various advanced mathematical concepts.
- Mastering radical notation opens a door to deeper understanding and problem-solving skills in algebra, geometry, and beyond.
Using Fractional Exponents:
Fractional exponents provide a graceful way to express roots and powers in a single, unified language. They offer a shortcut to simplify expressions, solve equations, and reveal hidden relationships between numbers. Let’s explore their essence and how to wield their power:
Bridging Roots and Exponents:
- Fractional exponents merge the concepts of roots and exponents.
- The numerator of the fraction represents the exponent.
- The denominator of the fraction represents the root.
Understanding the Syntax:
- An expression like x^(m/n) means the nth root of x raised to the power m.
- For example, 8^(2/3) signifies the cube root of 8 (which is 2) raised to the power 2, resulting in 4.
Key Rules for Manipulation:
- Converting to Radical Form: x^(m/n) = √(x^m) = (√x)^m
- Simplifying: Simplify the radical or exponent as needed.
- Multiplying: x^(m/n) * x^(p/q) = x^((mq + np)/nq)
- Dividing: x^(m/n) / x^(p/q) = x^((mq – np)/nq)
Examples in Action:
- 16^(1/4) = √(16) = 2 (fourth root of 16)
- 25^(3/2) = (√25)^3 = 5^3 = 125 (square root of 25 raised to the power 3)
- Simplify 9^(5/2): 9^(5/2) = (√9)^5 = 3^5 = 243
Unlocking Potential:
- Fractional exponents simplify complex expressions and reveal intriguing patterns.
- They are integral to advanced math concepts like calculus and differential equations.
- They appear in real-world applications like modeling growth and decay phenomena.
Which Method to Use When Multiplying Radicals?
The choice between radical notation and fractional exponents depends on personal preference, the specific problem, and desired outcome. Here’s a guide to help you decide:
Factors to Consider:
- Personal Comfort: Choose the method you feel most confident in.
- Simplicity of Expression: Fractional exponents can sometimes simplify expressions more than radical notation.
- Desired Outcome: If you need a final answer in radical notation, use that method.
- Context of the Problem: Some problems or mathematical fields might favor one notation over the other.
Key Considerations:
- Radical Notation:
- Emphasizes the root concept visually.
- Might be more intuitive for those familiar with roots.
- Can involve simplifying radicands to find perfect squares or cubes.
- Fractional Exponents:
- Offer a compact representation.
- Facilitate easier manipulation of exponents using rules of exponents.
- Might be preferred for those comfortable with exponents.
General Guidelines:
- Simple radicals: Radical notation is often efficient.
- Complex expressions or multiple roots: Fractional exponents can simplify calculations.
- Final answer requirement: Use the required notation.
Examples:
- Multiplying √5 and √7: Both notations work well.
- Simplifying √(x^5): Fractional exponents might be easier: (x^5)^(1/2) = x^(5/2).
- Solving equations involving radicals: Radical notation is often clearer.
Best Practice:
- Develop fluency in both methods to choose the most suitable one for each situation.
- Practice with various examples to gain confidence and understanding.
- Remember, the goal is to find the most efficient and accurate way to solve the problem.
How to Simplify Radical Expressions?
Simplifying radical expressions involves transforming them into their most compact and elegant forms, revealing their true essence. It’s like untangling a knotted string to reveal its smooth, flowing form. Here are the key steps:
Factor the Radicand:
- Break down the number or expression inside the radical symbol (the radicand) into its prime factors.
- Example: √72 = √(2 x 2 x 2 x 3 x 3)
Identify Perfect Square or Cube Factors:
- Look for pairs of identical prime factors that can be grouped together.
- If you find a factor that appears twice, you can move it outside the radical symbol as its square root.
- If a factor appears three times, you can move it outside as its cube root.
Move Factors Outside the Radical:
- For each perfect square factor, write its square root as a coefficient outside the radical.
- For each perfect cube factor, write its cube root as a coefficient outside the radical.
Simplify Further (Optional):
- If possible, simplify the resulting coefficient or radicand.
- Combine any like terms if necessary.
Example:
√72 = √(2 x 2 x 2 x 3 x 3) = √(2² x 3² x 2) = 2√(3²) x √2 = 6√2
Key Points:
- Only perfect square or cube factors can be moved outside the radical.
- Simplifying helps reveal patterns and relationships within expressions.
- It’s often useful for solving equations or performing further calculations.
Additional Tips:
- Practice factoring and identifying perfect squares and cubes.
- Use a calculator to check your simplifications.
- Try different examples to gain fluency in the process.
Why Use a Radical?
There are many reasons why using radicals can be beneficial in mathematics and beyond:
Expressing Roots:
- Radicals provide a concise and clear way to represent roots of numbers, specifically square roots, cube roots, and beyond.
- They are more elegant and efficient than writing out phrases like “the square root of” or “the cube root of”.
- This notation allows for easier manipulation and calculation with roots in equations and expressions.
Simplifying Expressions:
- Sometimes, using radicals can lead to simpler expressions compared to using rational or decimal values.
- Simplifying radicals often involves factoring the radicand and moving perfect squares or cubes outside the radical, resulting in a more compact form.
- This makes calculation and analysis easier and reveals underlying patterns within the expression.
Solving Equations:
- Many important equations in mathematics and physics involve radicals, especially quadratic equations with irrational roots.
- Understanding and manipulating radicals is crucial for solving these equations and finding their solutions.
- Radicals often appear in equations related to geometry, trigonometry, and other advanced mathematical fields.
Modeling Real-World Phenomena:
- In various scientific and engineering applications, concepts like growth rates, decay processes, and wave propagation can be described using mathematical models involving radicals.
- Understanding and manipulating radicals allows us to analyze and predict these real-world phenomena with greater accuracy.
Intellectual Challenge and Beauty:
- Exploring the world of radicals, their properties, and operations can be an intellectually stimulating and rewarding experience.
- Mastering their manipulation opens doors to solving complex problems and discovering hidden relationships within numbers.
- The elegance and simplicity of radical notation add a touch of beauty to the world of mathematics.
Overall, using radicals is not just a technical requirement in certain mathematical fields, but also a powerful tool for simplifying expressions, solving equations, modeling real-world phenomena, and unlocking the inherent beauty of numbers.
To Sum Up:
It seems like we’ve explored quite a bit about radicals and their intriguing presence in the world of math! To summarize the key points:
What are radicals?
- Notation using the √ symbol and a radicand (number or expression within it) to represent roots of numbers.
- Primarily used for square roots (√2), cube roots (√8), and other types of roots.
Benefits of using radicals:
- Expressing roots concisely: Simplifies phrases like “square root of” and allows for clearer representation.
- Simplifying expressions: Can lead to more compact forms compared to decimals or fractions.
- Solving equations: Crucial for handling equations involving irrational roots, especially quadratic equations.
- Modeling real-world phenomena: Used in equations for growth rates, decay processes, waves, and more.
- Intellectual challenge and beauty: Mastering radicals offers intellectual stimulation and unlocks hidden relationships in numbers.
Key Points for Simplifying Radicals:
- Factor the radicand to identify perfect squares or cubes.
- Move perfect squares or cubes outside the radical as their square or cube root, respectively.
- Simplify the resulting expression as needed.
Remember:
- Radicals are not just technical symbols but powerful tools for understanding and manipulating roots in various contexts.
- Simplifying radicals unlocks their elegance and opens doors to solving equations, modeling real-world phenomena, and appreciating the beauty of mathematics.
Follow Math Solver Online for more solutions