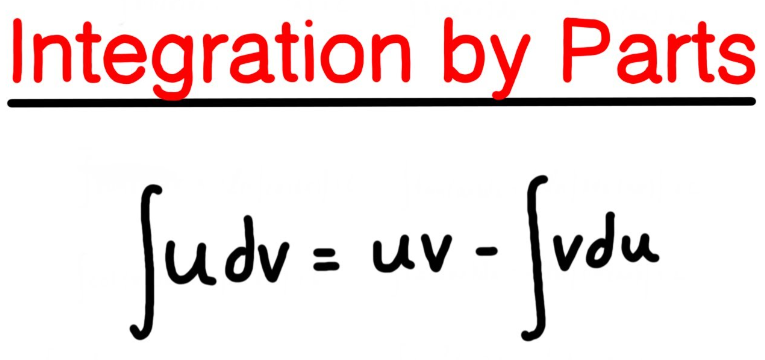In this article, we are discussing the Integration by Part Formula and how to do it. Integration, the mathematical act of reverse differentiation, unlocks the hidden areas tucked under the curves of functions. While many functions readily surrender their secrets under this process, certain cunning equations resist our direct attempts. To conquer these formidable foes, we must employ a strategic technique known as integration by parts. This powerful weapon leverages a clever partnership between two functions, strategically chosen and delicately manipulated, to dismantle the defenses of complex integrals. In the following exploration, we shall delve into the heart of this ingenious method, demystifying its underlying principles, unpacking its potent steps, and witnessing its triumphant applications in the face of seemingly insurmountable integrals. Buckle up, for we embark on a journey to conquer the unconquered, using the elegant blade of integration by parts!
When Substitution Doesn’t Work:
While substitution is a powerful tool in the integration toolbox, it doesn’t always win the day. There are instances where it throws up its hands and declares defeat, leaving us staring at a seemingly unyielding integral. Here are some reasons why substitution might fail:
- Lack of a Suitable Candidate: The crux of substitution hinges on finding a suitable function (u) and its derivative (du) that, when substituted into the integral, magically transform it into something easier to solve. But some integrals lack this magical partner, leaving us searching in vain for the perfect match.
- Circular Substitution: Sometimes, the substitution leads to an even more complex integral, involving the original function in a disguised form. This is like taking a roundabout that just circles back to where you started, wasting time and effort.
- Algebraic Intractability: Even if you find a suitable substitution, the resulting integral might become a beast of algebraic proportions, filled with cumbersome expressions and defying further simplification. This can be a dead end, as attempting to solve it might turn into a Sisyphean task.
- Exponential and Logarithmic Equations: Substitution struggles with certain integrals involving exponential and logarithmic functions. Their intricate relationships often demand more specialized techniques beyond the reach of basic substitution.
- Trigonometric Nightmares: While substitution can handle some trigonometric integrals, others with intricate combinations of sine, cosine, and tangent functions can become impenetrable fortresses under its watch. Specialized trigonometric identities and integration techniques are often needed for these complex beasts.
So, what do you do when substitution throws its towel in the ring? Fear not, for there are other heroes in the integration arena. Sometimes, integration by parts, integration by partial fractions, or even numerical methods might step up to save the day. The key is to recognize the limitations of substitution and be ready to deploy the appropriate weapon from your mathematical arsenal.
Examples when substitution doesn’t work:
Here are some examples of integrals where substitution doesn’t work effectively, along with explanations:
- Lack of Suitable Candidate:
- ∫ e^(x^2) dx
- Substitution doesn’t offer a simple function and its derivative that can transform the integral into a familiar form. Integration by parts or numerical methods are often used instead.
- Circular Substitution:
- ∫ sin(x^2) dx
- Trying substitution with u = x^2 leads to ∫ sin(u) * 1/(2√u) du, which still involves a trigonometric function and doesn’t simplify the problem. Other techniques, like trigonometric identities or numerical integration, might be more suitable.
- Algebraic Intractability:
- ∫ (x^3 + 1)/(x^5 + 2x + 3) dx
- Even with a substitution like u = x^5 + 2x + 3, the resulting integral becomes algebraically challenging and might not have a tractable solution using elementary functions.
- Exponential and Logarithmic Equations:
- ∫ x^2 ln(x) dx
- Substitution with u = ln(x) doesn’t lead to a simple integral. Integration by parts is typically used to handle this type of integral.
- Trigonometric Nightmares:
- ∫ sin^3(x) cos^4(x) dx
- Substitution with u = sin(x) or cos(x) doesn’t simplify the integral significantly. Trigonometric identities and techniques like integration by parts or reduction formulas are often necessary.
In these cases, alternative integration techniques, such as:
- Integration by parts
- Integration by partial fractions
- Trigonometric substitutions
- Trigonometric identities
- Numerical integration methods
Integration by Parts Formula:
Here’s the Integration by Parts Formula, along with equations and explanations:
Formula:
∫ u dv = uv – ∫ v du
Explanation:
- u and dv: The integral is broken down into two parts: u, a function that we can differentiate, and dv, a differential that we can integrate.
- uv: The product of u and the integral of dv (v).
- ∫ v du: The integral of v (the integral of dv) multiplied by the derivative of u (du).
Steps for Applying Integration by Parts:
- Identify u and dv:
- Choose u to be a function that becomes simpler when differentiated.
- Choose dv to be a differential that can be integrated easily.
- Differentiate u to find du:
- Calculate the derivative of u.
- Integrate dv to find v:
- Find the integral of dv.
- Apply the formula:
- Plug u, dv, v, and du into the formula ∫ u dv = uv – ∫ v du and simplify.
Example:
∫ x^2 ln(x) dx
- Let u = ln(x), so du = 1/x dx
- Let dv = x^2 dx, so v = (1/3)x^3
Applying the formula:
∫ x^2 ln(x) dx = (1/3)x^3 ln(x) – ∫ (1/3)x^3 * (1/x) dx = (1/3)x^3 ln(x) – (1/9)x^3 + C
How to Do Integration by Parts?
Here’s a guide on how to perform integration by parts, including equations and key steps:
Identify u and dv:
- Choose u: Select a part of the integrand that becomes simpler when differentiated.
- Choose dv: Pick the remaining part of the integrand that can be easily integrated.
General guidelines for choosing u:
- Prioritize inverse functions (like ln(x), arcsin(x), etc.)
- Consider exponential functions (like e^x)
- Opt for polynomials if trigonometric functions are involved
Differentiate u to find du:
- Calculate the derivative of the function you chose as u.
Integrate dv to find v:
- Find the integral of the expression you chose as dv.
Apply the formula:
- Use the integration by parts formula:
∫ u dv = uv – ∫ v du
- Substitute the values of u, dv, v, and du into the formula.
- Simplify the expression and evaluate the integral.
Example:
∫ x^2 e^x dx
- Let u = x^2 (becomes simpler when differentiated), so du = 2x dx
- Let dv = e^x dx (easy to integrate), so v = e^x
Applying the formula:
∫ x^2 e^x dx = x^2 e^x – ∫ e^x * 2x dx = x^2 e^x – 2 ∫ xe^x dx (repeated integration by parts might be needed for the new integral)
Putting the Formula To Work
Here are some examples of putting the integration by parts formula to work, along with equations and explanations:
- ∫ x^2 cos(x) dx
- Let u = x^2 (becomes simpler when differentiated), so du = 2x dx
- Let dv = cos(x) dx (easy to integrate), so v = sin(x)
Applying the formula:
∫ x^2 cos(x) dx = x^2 sin(x) – ∫ sin(x) * 2x dx = x^2 sin(x) + 2 cos(x) – 2C
- ∫ e^x sin(x) dx
- Let u = sin(x) (inverse function), so du = cos(x) dx
- Let dv = e^x dx (easy to integrate), so v = e^x
Applying the formula:
∫ e^x sin(x) dx = e^x sin(x) – ∫ e^x cos(x) dx (this new integral may need integration by parts again)
- ∫ ln(x) dx
- Let u = ln(x) (inverse function), so du = 1/x dx
- Let dv = dx (easy to integrate), so v = x
Applying the formula:
∫ ln(x) dx = x ln(x) – ∫ x * (1/x) dx = x ln(x) – x + C
Key points to remember:
- The choice of u and dv is crucial and often requires practice and intuition.
- Sometimes multiple applications of integration by parts are needed.
- Always simplify the resulting integral and add the constant of integration (C) at the end.
- Practice with various integrals to develop your skills and judgment in applying this technique effectively.
Where Does the Formula Come From?
The integration by parts formula has its roots in the fundamental relationship between differentiation and integration, expressed by the Fundamental Theorem of Calculus. It essentially states that differentiation and integration are “inverse” operations: taking the derivative of an integral will return the original integrand, and integrating the derivative of a function will give back the original function.
Here’s how the formula arises:
- Start with the product rule of differentiation: d(uv) = u’v + uv’
- Integrate both sides: ∫ d(uv) = ∫ (u’v + uv’) dx
- Rearrange the integral: ∫ u’v dx + ∫ uv’ dx = ∫ d(uv) dx
- Recognize the integrals on the left side: The first integral looks like the product of u and the integral of dv (uv), and the second integral looks like the integral of v multiplied by the derivative of u (v*du).
- Substitute and simplify: ∫ uv dx + ∫ v du dx = uv
- Rewrite the formula: uv – ∫ v du dx = ∫ u dv dx
This final equation is the familiar integration by parts formula. Therefore, it emerges from the basic principles of differentiation and integration, highlighting the interplay between these two fundamental operations.
Integration by Parts Practice
Here are some practice problems involving integration by parts, along with equations and explanations:
Problem 1:
∫ x arctan(x) dx
Solution:
- Let u = arctan(x), so du = 1/(1+x^2) dx
- Let dv = x dx, so v = (1/2)x^2
Applying the formula:
∫ x arctan(x) dx = (1/2)x^2 arctan(x) – ∫ (1/2)x^2 * 1/(1+x^2) dx = (1/2)x^2 arctan(x) – (1/4)ln(1+x^2) + C
Problem 2:
∫ e^x sin(x) dx
Solution:
- Let u = sin(x), so du = cos(x) dx
- Let dv = e^x dx, so v = e^x
Applying the formula:
∫ e^x sin(x) dx = e^x sin(x) – ∫ e^x cos(x) dx (this new integral needs integration by parts again)
Let u = cos(x), so du = -sin(x) dx Let dv = e^x dx, so v = e^x
∫ e^x sin(x) dx = e^x sin(x) – (e^x cos(x) + ∫ e^x sin(x) dx)
Rearranging:
2∫ e^x sin(x) dx = e^x sin(x) – e^x cos(x) ∫ e^x sin(x) dx = (1/2)(e^x sin(x) – e^x cos(x)) + C
Problem 3:
∫ x^3 ln(x) dx
Solution:
- Let u = ln(x), so du = 1/x dx
- Let dv = x^3 dx, so v = (1/4)x^4
Applying the formula:
∫ x^3 ln(x) dx = (1/4)x^4 ln(x) – ∫ (1/4)x^4 * 1/x dx = (1/4)x^4 ln(x) – (1/16)x^4 + C
To Sum Up:
Integration by parts is a powerful tool for conquering stubborn integrals that resist direct attacks. It leverages a clever partnership between two strategically chosen functions, their derivatives and integrals, to dismantle their defenses and unlock their secrets. We explored the formula, its derivation, and how to put it into practice with various examples.
Here’s a quick summary of our key takeaways:
- Formula: ∫ u dv = uv – ∫ v du
- Steps: Choose u and dv, differentiate u, integrate dv, and apply the formula
- Applications: Integrals involving inverse functions, exponentials, logarithms, and trigonometry
- Challenges: Choosing the right u and dv, handling complex resulting integrals
- Benefits: Overcoming challenges with substitution, unlocking diverse solutions
Remember, practicing and honing your intuition for choosing u and dv are crucial for mastering this technique. Keep tackling those tricky integrals, and integration by parts will be your loyal companion in your mathematical adventures!
Follow Math Solver Online for more solutions.